こんにちは。入試解説も停滞しておりましたが再開します。
芝国際中の大問2の(8)です。どの学校も同じですが、計算+文章題や図形の一行問題は確実に得点できるようにしておきたいですね。
問. 右(下)の図のように、半径8cmの円の円周を12等分しました。四角形ABCDの面積は何㎠ですか。
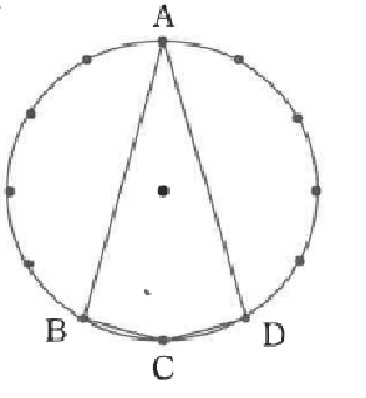
中心から各頂点へ半径を引くと、4つの三角形に分割できます。
この4つの三角形は円の半径を底辺として隣り合っている、または左右対称になっているため、
4つの三角形の面積は等しくなります。
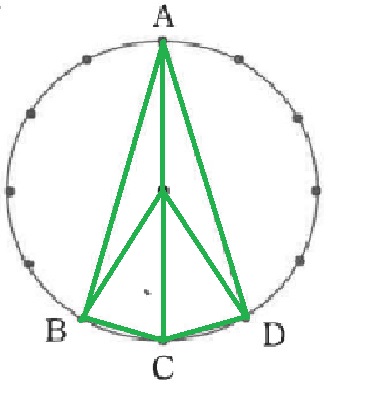
それではこのうち1つの三角形を取り上げて面積を求め、あとで4倍しましょう。
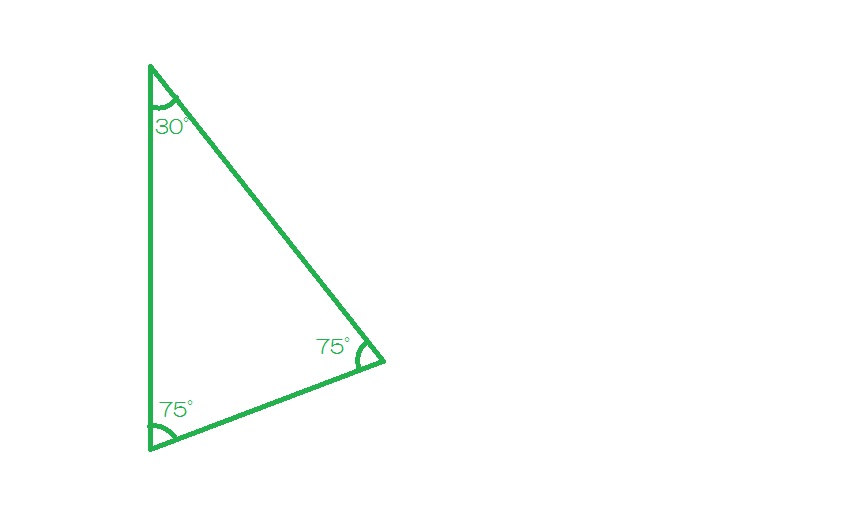
円を12等分しているので、右下の三角形は頂角30°の二等辺三角形になりますね。
となると、お決まりのパターンです。
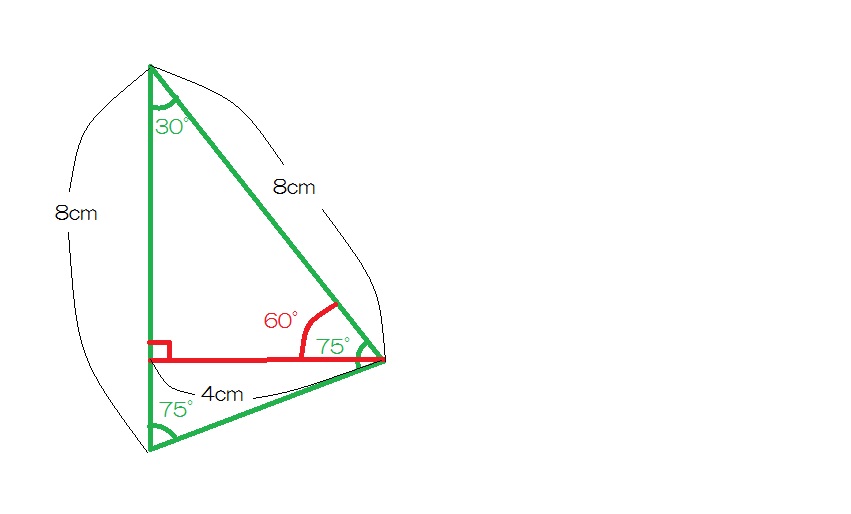
赤の補助線を引いて30°60°90°の直角三角形を作ると、4cmの高さが作れます。
よってこの三角形の面積は8×4÷2=16㎠、
求める四角形ABCDの面積はこの三角形4つ分なので16×4=64㎠
ちなみに先日芝国際中のオンライン説明会(塾対象)がありましたが、
やはり合否の分かれ目は一行問題とのお話しがありました。
ここで得点が伸び悩んでいる方、解決に向けて一緒に取り組みましょう!

