こんにちは。昨日の社会に続いて今日は数学。
大問3の関数は1次関数の出題でした。
2次関数の出題が多い単元ですが、2021年以来2年ぶりと
比較的短いスパンで出してきたのは少し意外です。
1次関数は中2で学習しているので、中2生も学年末テストが終わったら解いてみましょうね!
さて、問3の解説。
座標平面上の2つの三角形の面積の比から座標を求める問題です。
赤の三角形の面積が、青の三角形の面積の2倍になるような点Pを求めます。
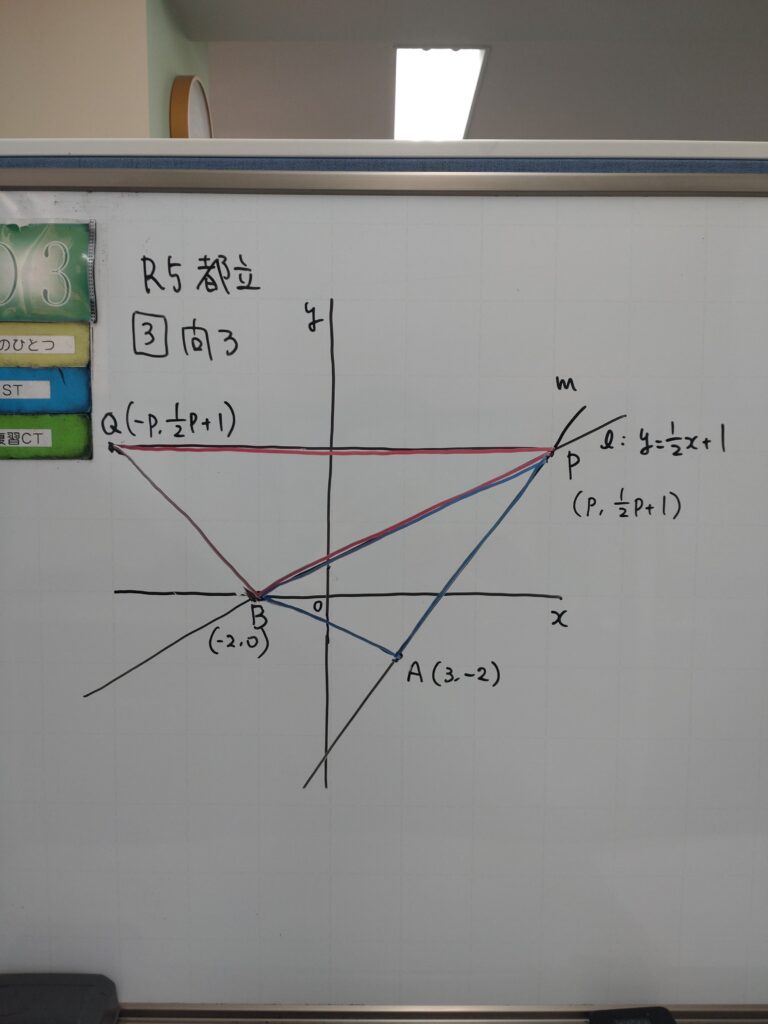
この手の問題の鉄則は求める点のⅹ座標を文字で置くこと、
通っている直線や放物線の式を使ってy座標も同じ文字で置くこと。
赤い三角形は求めやすいですが、青い三角形はすんなり求められませんね。
等積変形しましょう。
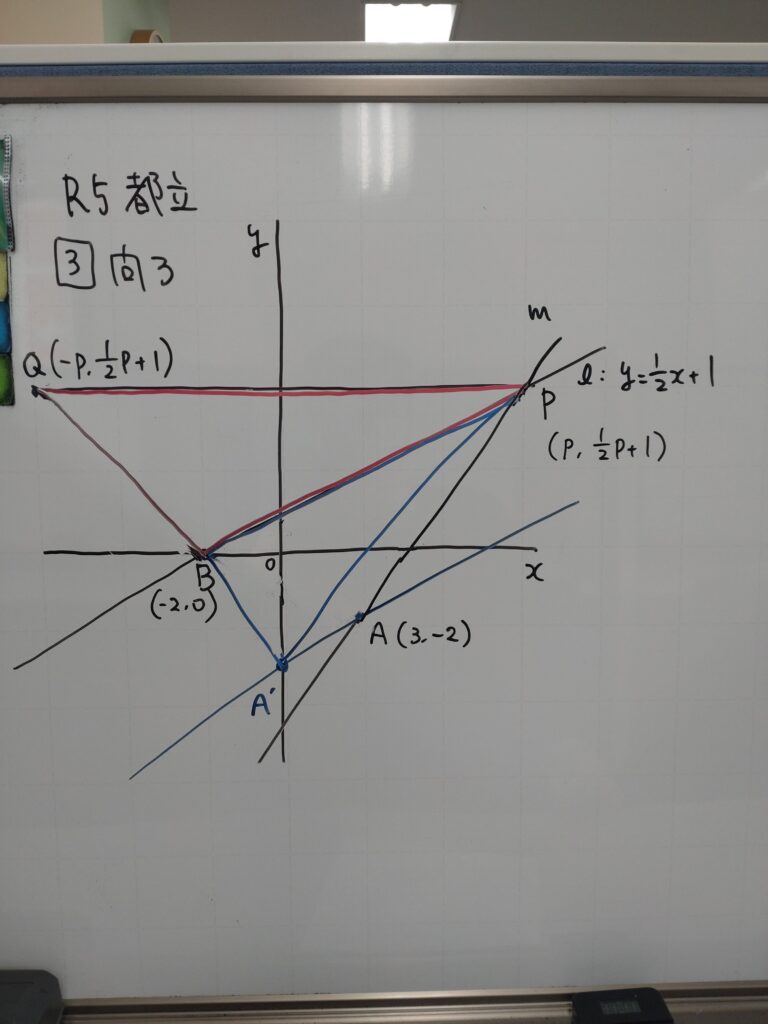
平行線を引いてAをA´に移すと面積が求めやすくなります。
(ⅹ軸上に移した方が分かりやすかったですね…)

関数の問3としては頻出の考え方なので、共通問題校で偏差値60以上の高校、
または数学で80点以上を取りたい人は類題演習必須です!!

