よく志望校に挙げられる近隣の私立中学校について、今年の入試問題の一部を解説していきます。
山脇は算数1科入試や国語1科入試の方式もあるので、ハイレベルな争いにはなりますが、
突出して1教科だけ得意な子にとっては狙い目かもしれません。
2025 A日程 算数 大問4
点PはAから、点QはBから同時に出発してそれぞれA,Bの間を一定の速さで繰り返し往復します。
グラフは点Pが出発してからの時間と点PからAまでの長さの変化を表したものです。
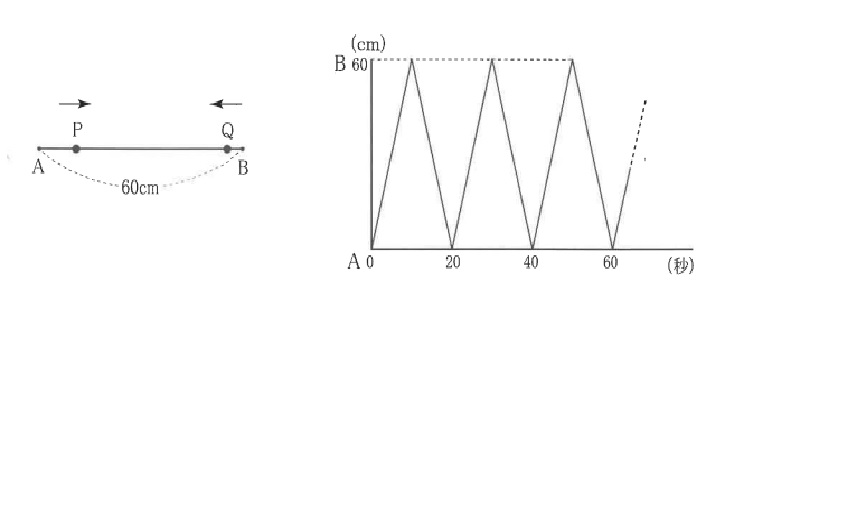
(1)②点Qの速さが毎秒2cmのとき、出発してから60秒間に点Pと点Qは何回重なりますか。
まずグラフから点Pの速さは 120cm÷20秒=毎秒6cm
また、60cm÷毎秒2cm=30秒 … (点Qが片道にかかる時間) よって点Qの運動もグラフに表すと
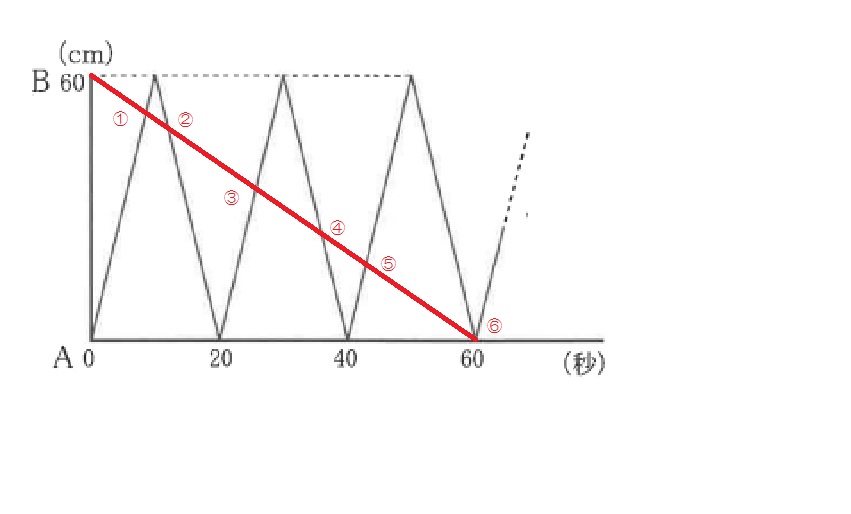
このように表すことができるので重なった回数は6回。
(2)点Pと点Qが出発してから60秒の間に5回重なるような点Qの速さは毎秒何cmですか。すべて求めなさい。ただし、点Qの速さは点Pの速さより遅いとします。
実際にグラフに適当に描いて交点を数えてみますが、ほとんどのパターンは元々描かれている点Pのグラフの3つの山を2回ずつ横切ることになるので計6回重なります。
これを5回にするには、山を横切らず、山の頂点(逆向きも含めて)で交わるように引くこと。
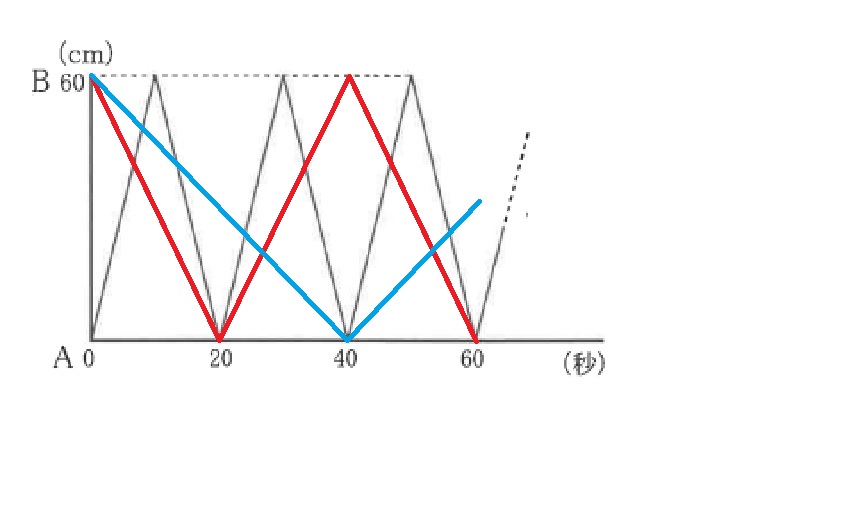
そうすると、0秒のBから①20秒のAに向かって、次に②40秒のAに向かって線を引き、
それに合わせて折り返していくと、60秒までの間に5回交わります。
60秒に向かって線を引くと前の問題と同じで6回交わるのでダメ。
よって答えは60cm÷20秒=毎秒3cm と 60÷40秒=毎秒1.5cm のとき。
山脇は速さとグラフの問題は頻出です。問題文の情報とグラフに落とし込んで、イメージしやすくしましょう。
解法が見つからない場合、とりあえず分かる情報を整理していくことで、手探りでも見つけられる可能性が広がります。

